Термодина́мика (греч. θέρμη — «тепло», δύναμις — «сила») — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника.
В термодинамике имеют дело не с отдельными молекулами, а с макроскопическими телами, состоящими из огромного числа частиц. Эти тела называютсятермодинамическими системами. В термодинамике тепловые явления описываются макроскопическими величинами — давление, температура, объём, …, которые не применимы к отдельным молекулам и атомам.
В теоретической физике наряду с феноменологической термодинамикой, изучающей феноменологию тепловых процессов, выделяют термодинамику статистическую, которая была создана для механического обоснования термодинамики и была одним из первых разделов статистической физики.
Термодинамика может быть применена в широком круге вопросов в области науки и техники, таких, как двигатели, фазовые переходы, химические реакции, явления переноса, и даже чёрные дыры. Термодинамика имеет важное значение для других областей физики и химии, химической технологии, аэрокосмической техники, машиностроения, клеточной биологии, биомедицинской инженерии, материаловедения, и полезно в таких других областях, как экономика.
Термодинамика исторически возникла как эмпирическая наука об основных способах преобразования внутренней энергии тел для совершения механической работы. Однако в процессе своего развития термодинамика проникла во все разделы физики, где возможно ввести понятие «температура» и позволила теоретически предсказать многие явления задолго до появления строгой теории этих явлени
Законы — начала термодинамики
Традиционно считается, что термодинамика основывается на четырёх законах (началах), которые сформулированы на основе экспериментальных данных и поэтому могут быть приняты как постулаты.
* 0-й закон — нулевое начало термодинамики: Постулирует существование термодинамического равновесия и вводит понятие абсолютной температуры.
Термодинамическое равновесие. Для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, которого она при фиксированных внешних условиях с течением времени самопроизвольно достигает. Если две изолированные системы  и
и  приведены в контакт друг с другом, то после достижения термодинамического равновесия полной системой
приведены в контакт друг с другом, то после достижения термодинамического равновесия полной системой 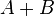 системы
системы  и
и  находятся в состоянии теплового (термического) равновесия друг с другом. При этом каждая из систем
находятся в состоянии теплового (термического) равновесия друг с другом. При этом каждая из систем  и
и  в отдельности также находится в состоянии термодинамического равновесия. Это равновесие не нарушится, если устранить контакт между системами, а затем восстановить его. Следовательно, если установление контакта между двумя системами
в отдельности также находится в состоянии термодинамического равновесия. Это равновесие не нарушится, если устранить контакт между системами, а затем восстановить его. Следовательно, если установление контакта между двумя системами  и
и  , которые до этого были изолированными, не приводит ни к каким изменениям, то эти системы находятся в тепловом равновесии друг с другом.
, которые до этого были изолированными, не приводит ни к каким изменениям, то эти системы находятся в тепловом равновесии друг с другом.
 и
и  приведены в контакт друг с другом, то после достижения термодинамического равновесия полной системой
приведены в контакт друг с другом, то после достижения термодинамического равновесия полной системой 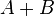 системы
системы  и
и  находятся в состоянии теплового (термического) равновесия друг с другом. При этом каждая из систем
находятся в состоянии теплового (термического) равновесия друг с другом. При этом каждая из систем  и
и  в отдельности также находится в состоянии термодинамического равновесия. Это равновесие не нарушится, если устранить контакт между системами, а затем восстановить его. Следовательно, если установление контакта между двумя системами
в отдельности также находится в состоянии термодинамического равновесия. Это равновесие не нарушится, если устранить контакт между системами, а затем восстановить его. Следовательно, если установление контакта между двумя системами  и
и  , которые до этого были изолированными, не приводит ни к каким изменениям, то эти системы находятся в тепловом равновесии друг с другом.
, которые до этого были изолированными, не приводит ни к каким изменениям, то эти системы находятся в тепловом равновесии друг с другом.
Закон транзитивности теплового равновесия. Если системы  и
и  находятся в тепловом равновесии и системы
находятся в тепловом равновесии и системы  и
и  находятся в тепловом равновесии, то системы
находятся в тепловом равновесии, то системы  и
и  также находятся в тепловом равновесии между собой. На основании этого закона делается вывод о существовании абсолютной температуры как термодинамического параметра, обладающего свойствами эмпирической температуры, но не зависящего от способа её измерения. Равенство температур есть условие теплового равновесия систем (или частей одной и той же системы).
также находятся в тепловом равновесии между собой. На основании этого закона делается вывод о существовании абсолютной температуры как термодинамического параметра, обладающего свойствами эмпирической температуры, но не зависящего от способа её измерения. Равенство температур есть условие теплового равновесия систем (или частей одной и той же системы).
 и
и  находятся в тепловом равновесии и системы
находятся в тепловом равновесии и системы  и
и  находятся в тепловом равновесии, то системы
находятся в тепловом равновесии, то системы  и
и  также находятся в тепловом равновесии между собой. На основании этого закона делается вывод о существовании абсолютной температуры как термодинамического параметра, обладающего свойствами эмпирической температуры, но не зависящего от способа её измерения. Равенство температур есть условие теплового равновесия систем (или частей одной и той же системы).
также находятся в тепловом равновесии между собой. На основании этого закона делается вывод о существовании абсолютной температуры как термодинамического параметра, обладающего свойствами эмпирической температуры, но не зависящего от способа её измерения. Равенство температур есть условие теплового равновесия систем (или частей одной и той же системы).
* 1-й закон — первое начало термодинамики: Представляет собой формулировку обобщённого закона сохранения энергии для термодинамических процессов. В наиболее простой форме его можно записать как
 ,
,
где 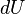 есть полный дифференциал внутренней энергии системы, а
есть полный дифференциал внутренней энергии системы, а  и
и  есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно. Нужно учитывать, что
есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно. Нужно учитывать, что  и
и  нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось.
нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось.
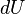 есть полный дифференциал внутренней энергии системы, а
есть полный дифференциал внутренней энергии системы, а  и
и  есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно. Нужно учитывать, что
есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно. Нужно учитывать, что  и
и  нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось.
нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось.
В литературе можно встретить и другие варианты приведённого выше соотношения, отличающиеся от него знаками ( или
или  ) перед
) перед  и
и  . Отличия вызваны тем, что конкретный вид этого уравнения зависит от соглашений, называемых «правилами знаков для работы и теплоты». Выше использовано «теплотехническое правило знаков для работы» (положительной считают работу, совершаемую системой, когда она отдаёт энергию, а отрицательной — работу, совершаемую над системой, когда она получает энергию) и «термодинамическое правило знаков для теплоты» (положительной считают теплоту, получаемую системой, а отрицательной — теплоту, отдаваемую системой). В «термодинамическом правиле знаков для работы» положительной считают работу, совершаемую над системой, а отрицательной — работу, совершаемую системой. Наконец, в «термохимическом правиле знаков для теплоты» положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой. Мнемоническое правило: в термодинамической системе знаков
. Отличия вызваны тем, что конкретный вид этого уравнения зависит от соглашений, называемых «правилами знаков для работы и теплоты». Выше использовано «теплотехническое правило знаков для работы» (положительной считают работу, совершаемую системой, когда она отдаёт энергию, а отрицательной — работу, совершаемую над системой, когда она получает энергию) и «термодинамическое правило знаков для теплоты» (положительной считают теплоту, получаемую системой, а отрицательной — теплоту, отдаваемую системой). В «термодинамическом правиле знаков для работы» положительной считают работу, совершаемую над системой, а отрицательной — работу, совершаемую системой. Наконец, в «термохимическом правиле знаков для теплоты» положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой. Мнемоническое правило: в термодинамической системе знаков 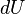 имеет тот же знак, что и энергия, передаваемая системе в виде работы или теплоты; в остальных случаях знак
имеет тот же знак, что и энергия, передаваемая системе в виде работы или теплоты; в остальных случаях знак 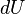 противоположен знаку передаваемой энергии. Стандарта, предписывающего использовать конкретный набор правил знаков, не существует, так что уместно рассматривать только степень распространённости того или иного правила в научной и учебной литературе. По этому поводу однозначно можно говорить лишь о том, что в современной литературе предпочитают использовать термодинамическое, а не термохимическое правило знаков для теплоты.
противоположен знаку передаваемой энергии. Стандарта, предписывающего использовать конкретный набор правил знаков, не существует, так что уместно рассматривать только степень распространённости того или иного правила в научной и учебной литературе. По этому поводу однозначно можно говорить лишь о том, что в современной литературе предпочитают использовать термодинамическое, а не термохимическое правило знаков для теплоты.
 или
или  ) перед
) перед  и
и  . Отличия вызваны тем, что конкретный вид этого уравнения зависит от соглашений, называемых «правилами знаков для работы и теплоты». Выше использовано «теплотехническое правило знаков для работы» (положительной считают работу, совершаемую системой, когда она отдаёт энергию, а отрицательной — работу, совершаемую над системой, когда она получает энергию) и «термодинамическое правило знаков для теплоты» (положительной считают теплоту, получаемую системой, а отрицательной — теплоту, отдаваемую системой). В «термодинамическом правиле знаков для работы» положительной считают работу, совершаемую над системой, а отрицательной — работу, совершаемую системой. Наконец, в «термохимическом правиле знаков для теплоты» положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой. Мнемоническое правило: в термодинамической системе знаков
. Отличия вызваны тем, что конкретный вид этого уравнения зависит от соглашений, называемых «правилами знаков для работы и теплоты». Выше использовано «теплотехническое правило знаков для работы» (положительной считают работу, совершаемую системой, когда она отдаёт энергию, а отрицательной — работу, совершаемую над системой, когда она получает энергию) и «термодинамическое правило знаков для теплоты» (положительной считают теплоту, получаемую системой, а отрицательной — теплоту, отдаваемую системой). В «термодинамическом правиле знаков для работы» положительной считают работу, совершаемую над системой, а отрицательной — работу, совершаемую системой. Наконец, в «термохимическом правиле знаков для теплоты» положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой. Мнемоническое правило: в термодинамической системе знаков 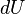 имеет тот же знак, что и энергия, передаваемая системе в виде работы или теплоты; в остальных случаях знак
имеет тот же знак, что и энергия, передаваемая системе в виде работы или теплоты; в остальных случаях знак 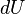 противоположен знаку передаваемой энергии. Стандарта, предписывающего использовать конкретный набор правил знаков, не существует, так что уместно рассматривать только степень распространённости того или иного правила в научной и учебной литературе. По этому поводу однозначно можно говорить лишь о том, что в современной литературе предпочитают использовать термодинамическое, а не термохимическое правило знаков для теплоты.
противоположен знаку передаваемой энергии. Стандарта, предписывающего использовать конкретный набор правил знаков, не существует, так что уместно рассматривать только степень распространённости того или иного правила в научной и учебной литературе. По этому поводу однозначно можно говорить лишь о том, что в современной литературе предпочитают использовать термодинамическое, а не термохимическое правило знаков для теплоты.
Иногда в рассматриваемое выражение для первого начала наряду с работой и теплотой включают ещё и работу переноса массы (химическую работу), выделяя её из общего выражения для работы в отдельное слагаемое.
* 2-й закон — второе начало термодинамики: Второй закон термодинамики исключает возможность создания вечного двигателя второго рода. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона.
1 — Постулат Клаузиуса. Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе. Это явление называют рассеиванием или диссипацией энергии.
Приведем второе начало термодинамики в ещё одной формулировке Рудольфа Юлиуса Клаузиуса (1865): для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния  , называемая энтропией, такая, что ее полный дифференциал
, называемая энтропией, такая, что ее полный дифференциал 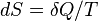 . [3]
. [3]
 , называемая энтропией, такая, что ее полный дифференциал
, называемая энтропией, такая, что ее полный дифференциал 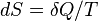 . [3]
. [3]
2 — Постулат Кельвина. Процесс, при котором работа переходит в теплоту без каких-либо других изменений в системе, является необратимым, то есть невозможно превратить в работу всю теплоту, взятую от источника с однородной температурой, не проводя других изменений в системе.
* 3-й закон — третье начало термодинамики: Теорема Нернста: энтропия любой равновесной системы при абсолютном нуле температуры всегда равна нулю (традиционная формулировка). Здесь важно различать аксиомы, отражающие законы природы, и имеющие исторические корни соглашения, необходимые для построения шкалы измерения соответствующей термодинамической величины. Так, аксиомами являются утверждения, что и энтропия, и температура есть односторонне ограниченные величины, и что своих граничных значений обе величины достигают одновременно. Согласно стандартным соглашениям принято, что и энтропия, и температура ограничены снизу, т. е. не могут быть меньше некоторых предельных значений. Из этого логично вытекают следующие соглашения, согласно которым наименьшее значение энтропии принято равным нулю, а наименьшее (нулевое) значение температуры служит реперной точкой для построения термодинамической шкалы температур.
Все термодинамические потенциалы имеют свои канонические наборы переменных и используются для анализа процессов при соответствующих условиях. Так, для изотермических изохорических процессов ( ) удобно использовать
) удобно использовать  , для изотермических изобарических (
, для изотермических изобарических (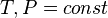 ) —
) — 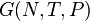 , а для изолированных систем (
, а для изолированных систем ( ) —
) —  .
.
 ) удобно использовать
) удобно использовать  , для изотермических изобарических (
, для изотермических изобарических (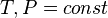 ) —
) — 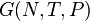 , а для изолированных систем (
, а для изолированных систем ( ) —
) —  .
.
Термодинамический потенциал  (энтропия)
(энтропия)
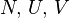 — независимые переменные;
— независимые переменные;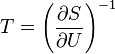 ;
;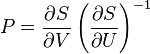 ;
; ;
;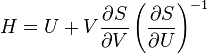 ;
; ;
; .
.
Термодинамический потенциал  (свободная энергия Гельмгольца)
(свободная энергия Гельмгольца)
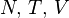 — независимые переменные;
— независимые переменные; ;
;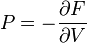 ;
; ;
;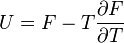 ;
; ;
;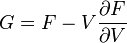 .
.
Термодинамический потенциал 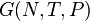 (энергия Гиббса)
(энергия Гиббса)
 — независимые переменные;
— независимые переменные;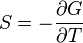 ;
; ;
; ;
;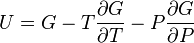 ;
;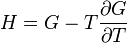 ;
; .
.
Термодинамический потенциал  (внутренняя энергия)
(внутренняя энергия)
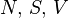 — независимые переменные;
— независимые переменные; ;
;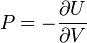 ;
; ;
;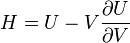 ;
;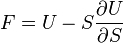 ;
;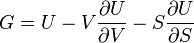 .
.
Фундаментальное уравнение Гиббса, экстенсивность и уравнение Гиббса — Дюгема
Выражение для полного дифференциала внутренней энергии называется фундаментальным уравнением Гиббса или просто уравнением Гиббса:
Значимость этого уравнения (и его более общих вариантов) состоит в том, что оно представляет собой тот фундамент, на котором базируется весь математический аппарат современной феноменологической термодинамики, как равновесной, так и неравновесной. По большому счёту, рассмотренные выше законы (начала) термодинамики нужны были именно для обоснования этого соотношения. Всю аксиоматику равновесной термодинамики можно свести к постулированию самого этого уравнения и свойств входящих в него термодинамических переменных.
С использованием других термодинамических потенциалов уравнение Гиббса можно переписать в следующих эквивалентных формах:
Среди термодинамических величин выделяют экстенсивные (внутренняя энергия, энтропия, объём и др.) и интенсивные (давление, температура и др.) величины. Величина называется экстенсивной, если ее значение для системы, сложенной из нескольких частей, равно сумме значений этой величины для каждой части. Предположением об экстенсивности термодинамических величин, однако, можно пользоваться, если рассматриваемые системы достаточно большие и можно пренебречь различными краевыми эффектами при соединении нескольких систем, например, энергией поверхностного натяжения. Пусть U (экстенсивная величина) является однородной функцией первого порядка от своих экстенсивных аргументов (математическое выражение аксиомы экстенсивности): для любого 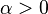
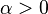
Для любой дифференцируемой однородной функции первого порядка  выполняется теорема Эйлера:
выполняется теорема Эйлера:
 выполняется теорема Эйлера:
выполняется теорема Эйлера:
Для энергии  теорема Эйлера имеет вид:
теорема Эйлера имеет вид:
 теорема Эйлера имеет вид:
теорема Эйлера имеет вид:
Отсюда легко следует уравнение Гиббса — Дюгема:
Это уравнение показывает, что между интенсивными переменными существует одна связь, являющаяся следствием предположения об аддитивности свойств системы. В частности, непосредственным следствием соотношений Гиббса-Дюгема является выражение для термодинамического потенциала Гиббса через химические потенциалы  компонент смеси:
компонент смеси:
 компонент смеси:
компонент смеси:Термодинамика сплошных сред
Приведённые выше формулировки аксиом термодинамики и соотношения для термодинамических потенциалов имеют место для простых моделей (сред) — для идеальных газов. Для более сложных моделей сред — упругих твердых сред, вязкоупругих сред, пластических сред, вязких жидкостей, сред с электромагнитными свойствами и других, законы термодинамики имеют более сложную формулировку, а термодинамические потенциалы формулируются в обобщенном виде с использованием тензоров[7][8][9][10]. В физике сплошных сред (физике континуума) термодинамика рассматривается как её составная часть, вводящая в рассмотрение переменные, характеризующие тепловые (термические) и химические свойства среды, и их связь с другими физическими величинами, а аксиомы термодинамики включаются в общую систему аксиом.

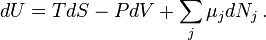




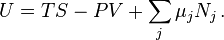


Комментариев нет:
Отправить комментарий